Research
Topological photonics in polariton lattices
Topology describes properties of a physical system that remain unaffected by distortion. The most straightforward example is the “genus”: the number of holes of a closed surface. For instance, a mug and a donut both have a hole, they both possess the same topological invariant (genus=1) and they can be transformed into each other via smooth deformations.
In solid state materials we can apply the same idea: we can define a topological invariant related to the properties of the electronic bands. Even though the bands and electronic eigenfunctions change when we deform the material, the topological invariant remains the same, and the only way to change it is by closing the gap between the bands. This has a very important consequence: when two materials with bands with different topological invariants are brought together, the gap needs to close exactly at the frontier between the materials. This means that an interface mode appears in the middle of the gap. As the existence of this “edge” mode is related to the topological properties of the bulk, it will always be there, no matter the shape of the region between the two materials. These concepts have explained the chiral edge transport in the quantum Hall effect, which is robust to disorder in the Hall bar, or the emergence of topological insulators that conduct only on their surface. 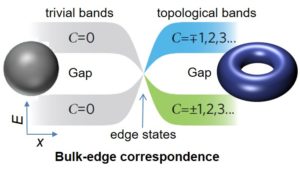
Implementing these ideas in photonics would be a promising route towards photonic devices with transport immune to scattering. Namely, photons in a topological lattice would be able to travel on the edge of the lattice no matter its shape. In the past few years, we have implemented polariton lattices with topological properties. In particular, we have addressed the physics of the honeycomb lattice, Fibonacci  potentials and the Su-Schrieffer-Heeger (SSH) lattice, and we have demonstrated the existence of edge states connected to the properties of the bulk. In the SSH lattice, we have obtained the first laser in a topological mode, and we have shown that it is robust to local perturbations of the photonic potential (see focus here).
potentials and the Su-Schrieffer-Heeger (SSH) lattice, and we have demonstrated the existence of edge states connected to the properties of the bulk. In the SSH lattice, we have obtained the first laser in a topological mode, and we have shown that it is robust to local perturbations of the photonic potential (see focus here).
- Topological photonics
T. Ozawa, H. M. Price, A. Amo, N. Goldman, M. Hafezi, L. Lu, M. Rechtsman, D. Schuster, J. Simon, O. Zilberberg, I. Carusotto, Rev. Mod. Phys. 91, 15006 (2019). [PDF] - Type-III and tilted Dirac cones emerging from flat bands in photonic orbital graphene
M. Milićević, G. Montambaux, T. Ozawa, O. Jamadi, B. real, I. Sagnes, A. Lemaître, L. Le Gratiet, A. Harouri, J. Bloch, A. Amo, Phys. Rev. X 9, 31010 (2019) [PDF] - Lasing in topological edge states of a 1D lattice
P. St-Jean, V. Goblot, E. Galopin, A. Lemaître, T. Ozawa, L. Le Gratiet, I.Sagnes, J. Bloch, A. Amo, Nat. Photon. 11, 651 (2017). [PDF] [PDF Suppl.] see focus - Exploring topological edge states in photonic quasicrystals
F. Baboux, E. Levy, A. Lemaître, C. Gomez, E. Galopin, L. Le Gratiet, I. Sagnes, A. Amo, J. Bloch, and E. Akkermans, , Phys. Rev. B 95, 161114(R) (2017). [PDF] [PDF Suppl.] - Orbital edge states in a photonic honeycomb lattice
M. Milićević, T. Ozawa, G. Montambaux, I. Carusotto, E. Galopin, A. Lemaître, L. Le Gratiet, I. Sagnes, J. Bloch, and A. Amo, Phys. Rev Lett. 118, 107403 (2017). [PDF] [PDF Suppl.] - Spin-Orbit Coupling for Photons and Polaritons in Microstructures
V. G. Sala, D. D. Solnyshkov, I. Carusotto, T. Jacqmin, A. Lemaître, H. Terças, A. Nalitov, M. Abbarchi, E. Galopin, I. Sagnes, J. Bloch, G. Malpuech, and A. Amo, Phys. Rev. X 5, 011034 (2015). [PDF] [PDF Suppl.] - Direct observation of Dirac cones and a flatband in a honeycomb lattice for polaritons
T. Jacqmin, I. Carusotto, I. Sagnes, M. Abbarchi, D. Solnyshkov, G. Malpuech, E. Galopin, A. Lemaître, J. Bloch, A. Amo, , Phys. Rev. Lett. 112, 116402 (2014). [PDF] [PDF Suppl.]
Wave turbulence in polariton fluids
In a classical fluid turbulence describes the redistribution of the energy injected in the system from large length-scales to small length-scales. The most popular manifestation of this phenomenon is the appearance of vortices and eddies in turbulent flow of water.
In a photon fluid, the great challenge to observe turbulent phenomena has been to obtain strong enough interactions. Polaritons in microcavities have proved to be ideal to study this kind of physics. The demonstration of polariton superfluidity and the nucleation of vortices and solitons have been the first steps in the investigation of turbulent cascades in fluids of light, and it is one of our active research lines.
- Phase-controlled bistability of a dark soliton train in a polariton fluid
V. Goblot, H. S. Nguyen, I. Carusotto, E. Galopin, A. Lemaître, I. Sagnes, A. Amo, and J. Bloch, Phys. Rev. Lett. 117, 217401 (2016). [PDF] [PDF Suppl.] - Acoustic Black Hole in a Stationary Hydrodynamic Flow of Microcavity Polaritons
H. S. Nguyen, D. Gerace, I. Carusotto, D. Sanvitto, E. Galopin, A. Lemaître, I. Sagnes, J. Bloch, A. Amo, , Phys. Rev. Lett. 114, 036402 (2015). [PDF] [PDF Suppl.] - Polariton superfluids reveal quantum hydrodynamic solitons

A. Amo, S. Pigeon, D. Sanvitto, V.G. Sala, R. Hivet, I. Carusotto, F. Pisanello, G. Lemenager, R. Houdre, E. Giacobino, C. Ciuti, A. Bramati, Science 332, 1167 (2011). - All-optical control of the quantum flow of a polariton superfluid
D. Sanvitto, S. Pigeon, A. Amo, D. Ballarini, M. D. Giorgi, I. Carusotto, R. Hivet, F. Pisanello, V. G. Sala, P. S. Soares-Guimaraes, R. Houdré, E. Giacobino, C. Ciuti, A. Bramati, G. Gigli, All-optical control of the quantum flow of a polariton superfluid, Nature Phot. 5, 610 (2011). - Superfluidity of polaritons in semiconductor microcavities
A. Amo, J. Lefrère, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdré, E. Giacobino, A. Bramati, Nature Phys. 5, 805 (2009).