Topological lasing
Our group in collaboration with Tomoki Ozawa from the Università di Trento in Italy, has recently obtained lasing in topological edge states. Such a laser implements a resonating mode that is intrinsically protected, thanks to the topological properties of its architecture, against external perturbations and fabrication defects.
The discovery of topological phase transitions in condensed matter, which was awarded the 2016 Noble prize in physics, has profoundly influenced the field of solid-state physics. The hallmark of these phase transitions is the emergence of localized states whose properties are unaffected by the presence of defects, dislocations and other kinds of disorder. For example, topological insulators, which are one of the most notable manifestations of these exotic phases, present an electrical conductivity along their edge that is perfectly insensible to the presence of irregularities. Recently the extension of this concepts to the realm of photonics has triggered considerable efforts to engineer a new generation of optical devices (e.g. waveguides, optical isolators, diodes, and, of course, lasers) whose performances are unaffected by perturbations of their environment.
In our group we have realised a topologically robust laser by taking profit of the physics of cavity polaritons, a half-light /half-matter quasi-particle confined in cylindrically-shaped optical cavities (see the figure on the right). By coupling these micro-cylinders together, we have fabricated a one-dimensional lattice that presents well-defined topological properties leading to the emergence of localized photonic modes at the edges of this lattice.
The lattice we fabricated implements the Su-Schrieffer-Heeger Hamiltonian for polaritons, which is the simplest Hamiltonian showing topological properties. The lattice can be arranged in two different configurations characterised by two different topological invariants: 0 and 1. The second arrangement is topologically non-trivial, and presents topological edge states whose existence and energy is protected against certain deformations of the lattice. Then, by using the gain associated to the matter part of polaritons, we triggered laser emission from one of these modes, thus realizing a topological laser.
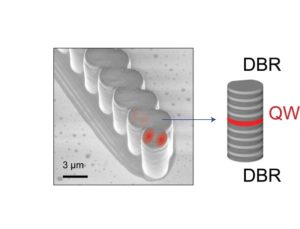
Scanning electron microscope image of the polariton SSH chained employed for the observation of 1D topological lasing.
Our realisation is the first 1D topological laser ever reported, and it profits from the topological properties of the Su-Schrieffer-Heeger (SSH) Hamiltonian. Following a similar configuration but this time using coupled ring resonators, the group of Liang Feng at the University of Pennsilvania and the group of Mercedeh Khajavikhan at CREOL have also reported lasing in 1D structures implementing the SSH Hamiltonian. A note on these three works can be found in the December 2018 issue of Optics and Photonics News.
Almost simultaneously to the publication of these works, three different reports showed lasing in the topological edge states of 2D photonic lattices. The group of Boubacar Kante at UCSD reported a 2D topological laser whose chiral edge states arise from the breaking the time reversal symmetry in a 2D photonic crystal. The groups of Mercedeh Khajavikhan at CREOL and Moty Segev at Technion have reported robust edge state lasing in a 2D array of coupled ring resonators implementing the photonic version of the Quantum spin Hall effect. Finally, the group of Sven Hofling from the University of Wurzburg have presented indications of lasing in topological edge states in a polariton honeycomb lattice. These discoveries push the field of topological photonics to the area of integrated lasers, opening the way to new architectures intrinsically robust to imperfections.
1D topological lasers:
Lasing in topological edge states of a 1D lattice, P. St-Jean, V. Goblot, E. Galopin, A. Lemaître, T. Ozawa, L. Le Gratiet, I.Sagnes, J. Bloch and A. Amo, Nat. Photon. 11, 651 (2017).
Topological hybrid silicon microlasers, H. Zhao, P. Miao, M. H. Teimourpour, S. Malzard, R. El-Ganainy, H. Schomerus, and L. Feng, Nat. Commun. 9, 981 (2018).
Edge-Mode Lasing in 1D Topological Active Arrays, M. Parto, S. Wittek, H. Hodaei, G. Harari, M. A. Bandres, J. Ren, M. C. Rechtsman, M. Segev, D. N. Christodoulides, and M. Khajavikhan, , Phys. Rev. Lett. 120, 113901 (2018).
2D topological lasers:
Nonreciprocal lasing in topological cavities of arbitrary geometries, B. Bahari, A. Ndao, F. Vallini, A. El Amili, Y. Fainman, and B. Kanté, Science 358, 636 (2017).
Topological insulator laser: Experiments, M. A. Bandres, S. Wittek, G. Harari, M. Parto, J. Ren, M. Segev, D. N. Christodoulides, and M. Khajavikhan, Science 359, aar4005 (2018).
Exciton-polariton topological insulator, S. Klembt, T. H. Harder, O. A. Egorov, K. Winkler, R. Ge, M. A. Bandres, M. Emmerling, L. Worschech, T. C. H. Liew, M. Segev, C. Schneider, and S. Höfling, Nature 562, 552 (2018).